Adunarea unui sir de numere naturale, consecutive, copilul poate sa o intalneasca la clasa la capitolul ”Adunarea numerelor naturale”, la exercitii cu gruparea convenabila a termenilor (pentru a putea aduna mai usor) sau la concursuri scolare.
Un astfel de exercitiu arata cam asa:
1 + 2 + 3 + ... + 100 = ? (suma lui Gauss)
Prima intrebare a parintelui este:
Poate copilul meu sa rezolve asa ceva in clasa a IV-a?
Raspunsul meu: Daca i-a explicat doamna, DA. Daca nu sau daca nu a inteles, s-ar putea sa fie nevoie sa o faceti voi si mai jos gasiti cateva sugestii.
Precizare: Rezolvarea de mai jos este valabila pentru adunarea unui sir de numere naturale, consecutive in care primul termen este 1.
Varianta 1 - primul numar este 1, ultimul numar al sirului este par (ex.: 100)
a) prin grupare
1 + 2 + 3 + ... + 100 = ?
Scriem acest sir astfel incat sa avem primii trei termeni si ultimii trei termeni ai sirului (pentru a putea grupa termenii):
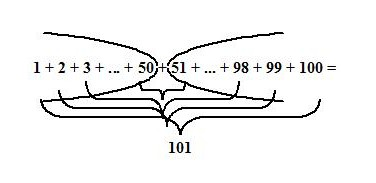
1 + 2 + 3 + ... + 98 + 99 + 100 = ?
Adunam primul cu ultimul termen -> 100 + 1 = 101,
continuam si adunam termenul al doilea cu penultimul numar -> 99 + 2 = 101,
continuam, termenul al treilea cu antepenultimul numar -> 98 + 3 = 101
astfel, observam ca grupand termenii vom avea perechi de numere a caror suma este 101.
Intrebarea este cate perechi?
In cazul in care sunt 100 de numere, grupate in perechi atunci vom avea 100 : 2 = 50 (perechi)
Deci rezolvarea este:
101 x 50 = 5050
b) cu ajutorul unei formule
1 + 2 + 3 + ...+ n = ( n + 1 ) x ( n : 2) = (n + 1) x n : 2 (am desfacut parantezele ca nu aveau sens in formula finala, o sa vedeti mai jos de ce ...)
unde n = numar natural par
iar exercitiul de mai sus devine foarte simplu:
1 + 2 + 3 + ... + 100 = (100+1) x (100:2) = 101 x 50 = 5050
Varianta 2 - primul numar este 1, ultimul numar al sirului este impar (ex.: 99)
a) prin grupare
1 + 2 + 3 + ... + 99 = ?
Scriem, din nou, acest sir astfel incat sa avem primii trei termeni si ultimii trei termeni ai sirului:
1 + 2 + 3 + ... + 97 + 98 + 99 =
Adunam primul cu ultimul termen -> 99 + 1 = 100,
continuam si adunam termenul al doilea cu penultimul numar -> 98 + 2 = 100,
continuam, termenul al treilea cu antepenultimul numar -> 97 + 3 = 100
astfel, grupand termenii vom avea perechi de numere a caror suma este 100.
Intrebarea importanta este cate perechi?
In cazul in care sunt 99 de numere, grupate in perechi atunci putem folosi 2 rationamente:
a) numar de perechi se poate afla
(99 - 1) : 2 = 98 : 2 = 49, deci daca am avea 98 de numere am avea 49 de perechi
(99 + 1) : 2 = 100 : 2 = 50, deci daca am avea 100 de numere am avea 50 de perechi (astfel vedem unde este mijlocul sirului)
dar noi avem 99 de numere, deci putem face urmatorul desen:
Pe desen vedem ca mijlocul sirului este 50, deci ultima pereche este 49 + 51 = 100, rezulta 49 perechi.
b) mai simplu numarul de perechi este (99 - 1): 2 = 49, motivul este acela ca impartirea cu 2 nu se poate face decat dintr-un numar par, atunci numarul par mai mic decat 99 este 98.
Dupa ce am aflat ca numarul de perechi este 49, nu trebuie sa uitam ca a ramas un numar fara pereche, acela este 50.
Deci rezolvarea este:100 x 49 + 50 = 4900 + 50 = 4950
b) cu ajutorul unei formule
nr. de perechi mijlocul sirului
1 + 2 + 3 + ... + n = (n + 1) x (n - 1) : 2 + [(n - 1) : 2 + 1] = n x (n + 1) : 2 (daca nu ma credeti faceti inmultirile)
unde n = numar natural impar
iar exercitiul de mai sus devine foarte simplu:
1 + 2 + 3 + ... + 99 = 99 (99 + 1) : 2 =99 x 100 : 2 = 9900 : 2 = 4950
Observam ca este aceeasi formula ca in varianta 1. Atunci fie copilul rezolva prin gruparea termenilor si cu ajutorul mijlocului sirului, fie memoreaza formula ca atare (Copilul meu prefera varianta cu mijlocul sirului, deoarece dupa un timp, iar uita formula.).
Asa cum am precizat mai sus aceasta metoda este utila pentru sirurile care au primul termen 1, in cazul in care primul termen este un alt numar, lucrurile se complica, dar nu cred ca este chiar de clasa a IV-a exercitiul de mai jos:
......Actualizare 10.12.2013.......
Tot o varianta cu cate putin din tot ce este mai sus, folosita intens in clasa a V-a este cea cu dublarea sirului:
-se scrie sirul nostru pe primul rand, iar pe randul al doilea acelasi sir, dar in ordine inversa si apoi se aduna celor doua siruri astfel:
ex. 1)
1 + 2 + 3 + ... + 100 S1 = sirul 1 (de rezolvat)
100 + 98 + 97 + ... + 1 S2 = sirul 2 ("inversul")
----------------------------
101 + 101 + 101+...+101 S1+S2
S1+S2 = 2 x S (pentru ca avem aceeasi termeni in ambele siruri, iar la adunare nu conteaza ordinea termenilor)
2S= 101 + 101 + 101 + ... + 101 (de atatea ori cati termeni avem, Nt = 100)
2S = 101x100 = 10100
daca 2S = 10100,
atunci S = 10100 : 2,
S = 5050 (adica sirul nostru) 1 +2 + 3 + ... + 100 = 5050
(aceasta completare este pentru cei care cauta acul in carul cu fan, cum am facut-o si eu de atatea ori)
..................................................
Exemplul nostru de mai sus:
1 + 2 + 3 + ... + 99 = s-ar rezolva astfel:
mijlocul sirului, x = 50 (reiese clar din desen)
numarul de termeni Nt = 99 (dupa formula de mai sus -> 99-1+1 = 99
atunci
1+ 2 + 3 + ... + 99 = 50 x 99 = 4950
In concluzie putem calcula sirurile de numere naturale consecutive in mai multe variante, dar provocarea rezervata noua parintilor este de a-l atrage pe cel mic in diferite jocuri cu ajutorul carora isi va insusi temeinic multe notiuni, iar in acelasi timp ne si putem distra impreuna.
Daca nu ati gasit tot ce va interesa incercati si articolul Cum aflam un termen al sirului? Cum adunam un sir de numere care nu sunt consecutive?
Actualizare 10.12.2013
Varianta 3 - sir de numere consecutive
27 + 28 + .... + 97 = ?
Acest sir se poate rezolva foarte usor cu urmnatoarea formula
t1 + t2 + t3 + ... + tn = (t1 + tn) x Nt : 2, unde
t1 = primul termen
tn = ultimul termen
Nt = numarul de termeni ai sirului (aici gasiti mai multe explicatii - mie mi-a placut cel mai mult partea in care explica cum se afla numarul de termeni dintr-un sir de numere consecutive, ceea ce este de folos si pentru clasa a IV-a -> (tn-t1) + 1 )
rezolvarea sirului propus 27 + 28 + ... + 97 = (27 + 97) (97-27+1) : 2 = 124 x 71 : 2 = 4402,
putem aplica aceasta formula si pentru variantele prezentate mai sus:
varianta 1
1 + 2 + 3 + ... + 100 = (100+1) x (100-1+1) : 2 = (100 + 1) x 100 : 2, rezulta chiar formula de mai sus, ca un caz special
varianta 2
1 + 2 + 3 + ... + 99 = (99 + 1) x (99-1+1) : 2 = (99+1) x 99 : 2, aceeasi concluzie, daca scriem sub forma 99 (99+1):2
Deci varianta 3 se aplica pentru siruri de numere naturale consecutive, iar variantele 1 si 2 sunt cazuri particulare ale acesteia.
......Actualizare 10.12.2013.......
Tot o varianta cu cate putin din tot ce este mai sus, folosita intens in clasa a V-a este cea cu dublarea sirului:
-se scrie sirul nostru pe primul rand, iar pe randul al doilea acelasi sir, dar in ordine inversa si apoi se aduna celor doua siruri astfel:
ex. 1)
1 + 2 + 3 + ... + 100 S1 = sirul 1 (de rezolvat)
100 + 98 + 97 + ... + 1 S2 = sirul 2 ("inversul")
----------------------------
101 + 101 + 101+...+101 S1+S2
S1+S2 = 2 x S (pentru ca avem aceeasi termeni in ambele siruri, iar la adunare nu conteaza ordinea termenilor)
2S= 101 + 101 + 101 + ... + 101 (de atatea ori cati termeni avem, Nt = 100)
2S = 101x100 = 10100
daca 2S = 10100,
atunci S = 10100 : 2,
S = 5050 (adica sirul nostru) 1 +2 + 3 + ... + 100 = 5050
(aceasta completare este pentru cei care cauta acul in carul cu fan, cum am facut-o si eu de atatea ori)
..................................................
Noi ne-am jucat mai multe zile cu sirurile pentru a putea fi asimilate toate informatiile de mai sus si am facut pe rand, jocul d-na invatatoare - elevul nestiutor, iar eu cateodata intelegeam asa de greu ... . Iar bonus i-am oferit urmatorul truc sa-l joace cu colegii si sa calculeze rapid in memorie suma a 5 numere consecutive:
- se scriu pe o foaie numerele
- copilul se uita la numarul din mijloc (al treilea) si il inmulteste cu cinci
- pentru a putea face inmultirea repede, in memorie, trebuie sa descompuna termenul inmultit in doua numere usor de inmultit cu 5
ex.
25, 26, 27, 28, 29
27 x 5 = 20 x 5 + 7 x 5 = 100 + 35 = 135 (exercitii de acest tip s-au facut multe la scoala, deci ce prilej mai bun pentru repetare si cresterea abilitatilor la calcul rapid?)
Explicatia matematica si alte trucuri interesante le gasiti aici. (Imi pare rau, dar informatiile din acest articol sunt doar in engleza. La metoda 2 este o greseala in poza, dar in explicatie totul este corect.)
Explicatia matematica si alte trucuri interesante le gasiti aici. (Imi pare rau, dar informatiile din acest articol sunt doar in engleza. La metoda 2 este o greseala in poza, dar in explicatie totul este corect.)
Ceea ce mi s-a parut foarte util la trucul 2 pe care eu l-am transformat in joc pentru copilul meu, este ca pentru orice sir de numere consecutive, cu un numar impar de termeni si la care cunoastem: mijlocul sirului si numarul de termeni putem afla foarte usor suma.
Exemplul nostru de mai sus:
1 + 2 + 3 + ... + 99 = s-ar rezolva astfel:
mijlocul sirului, x = 50 (reiese clar din desen)
numarul de termeni Nt = 99 (dupa formula de mai sus -> 99-1+1 = 99
atunci
1+ 2 + 3 + ... + 99 = 50 x 99 = 4950
In concluzie putem calcula sirurile de numere naturale consecutive in mai multe variante, dar provocarea rezervata noua parintilor este de a-l atrage pe cel mic in diferite jocuri cu ajutorul carora isi va insusi temeinic multe notiuni, iar in acelasi timp ne si putem distra impreuna.
Daca nu ati gasit tot ce va interesa incercati si articolul Cum aflam un termen al sirului? Cum adunam un sir de numere care nu sunt consecutive?
Actualizare 10.12.2013




12 comentarii:
Foarte explicit și util. Mulțumim!
Multumim ! clar si pe intelesul nostru
multumim de ajutor!
ma ajuta i si pe mn va rog frumos [(8-2)*(3+2)]+100:(7+3)
[(8-2)*(3+2)]+100:(7+3)=(6*5)+100:10=30+100:10=30+10=40.
Buna ziu. Am si eu nevoie de ajutor. Un exercitiu de clasa a 5-a, pe care sincer nu il inteleg. Fie numarul a= 12345678910...999, unde cifrele sunt obtinute folosind numere de la 1 la 999. Care este a 1996-a cifra ?
Sincer eu nu gasesc nici un rationament al sirului si nu stiu daca un copil de 11-12 ani ar putea sa perceapa asa ceva. Exercitul este din o carte de matematica, nicidecum vreo culegere. Va multumesc!
Cand nu aveti nicio idee. Puneti exercitiul in bara motorului de cautare si veti gasi undeva raspunsul. E cel mai rapid decat sa asteptati (ca la mine pe blog :) un raspuns care poate veni mult prea tarziu.
Pentru exemplificare, am copiat textul scris de dumneavoastra in bara Google si am obtinut, rapid o ”frumusete” de rezolvare (sursa mateonline.net - forum matematic - vizitator)
NUMERELE DE LA 1 LA 9 SUNT PE POZITIA K, UNDE K E ACEL NUMAR (1-9)
NUMERELE DE LA 10 LA 99 SUNT PE POZITIILE 2K-10 (PRIMA CIFRA) SI 2K-9 (A DOUA CIFRA), UNDE K ESTE ACEL NUMAR (10-99) - VERIFICAM PT 99: POZITIILE: 2*99-10=188 SI 2*99-9=189, 189<1996
NUMERELE DE LA 100 LA 999 SUNT PE POZITIILE 3K-110, 3K-109 SI 3K-108, UNDE K ESTE ACEL NUMAR (100-999) - VERIFICAM PENTRU 199: POZITIILE: 3*199-110=487, 3*199-109=488, 3*199-108=489
NUMARUL 999 OCUPA POZITIILE: 3*999-110=2887, 3*999-109=2888, 3*999-108=2889, 2889>1996, REZULTA CA POZITIA 1996 ESTE IN GRUPA SUTELOR
DECI SE CAUTA NUMARUL NATURAL K, A CAREI POZITIE 3K-(110 SAU 109 SAU 108) = 1996
3K-110=1996 => K=702, RESTUL NU SUNT NUMERE INTREGI
MAI VERIFICAM ODATA PENTRU NUMARUL 701 CARE OCUPA POZITIILE 3*701-110=1993, 3*701-109=1994, 3*701-108=1995
DECI POZITIA 1996 ESTE OCUPATA DE CIFRA 7 DIN NUMARUL 702.
Daca veti cauta si dumneavoastra veti mai gasi niste rezolvari interesante in acelasi loc (ideea de plecare a lor este aceeasi studiul modului in care se repeta cifrele pe intervale 1-10, 10-20 etc.).
Sper ca v-am ajutat mai mult asa decat daca vi-l rezolvam eu. :)
Daaa. Va multumesc, oricum ptr un elev ce a terminat clasa a4-a , imi pare extrem de derutant exercitiul.
Sunteti cumva la clasa a V a B de la Scoala Centrala?
Nu.
Multumim! De mare ajutor!
Trimiteți un comentariu
Pe acest blog vor fi afisate doar comentariile care folosesc un limbaj adecvat si au legatura cu subiectele prezentate.